Der Kosinussatz lautet bekanntlich:
(1) ![]()
Dabei sind ![]() und
und ![]() die Seiten eines allgemeinen Dreiecks und
die Seiten eines allgemeinen Dreiecks und ![]() der der Seite
der der Seite ![]() gegenüberliegende Winkel:
gegenüberliegende Winkel:
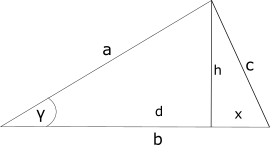
Die Höhe ![]() steht senkrecht auf der Seite
steht senkrecht auf der Seite ![]() und teilt diese in zwei Abschnitte
und teilt diese in zwei Abschnitte ![]() und
und ![]() ,
, ![]() . In einem rechtwinkligen Dreieck ist der Kosinus gleich dem Verhältnis von Ankathete zu Hypotenuse. Betrachtet man hier das von den Seiten
. In einem rechtwinkligen Dreieck ist der Kosinus gleich dem Verhältnis von Ankathete zu Hypotenuse. Betrachtet man hier das von den Seiten ![]() und
und ![]() gebildete rechtwinklige Dreieck, so gilt
gebildete rechtwinklige Dreieck, so gilt ![]() oder
oder ![]() .
.
Auf die durch ![]() und
und ![]() bzw.
bzw. ![]() und
und ![]() gebildeten rechwinkligen Dreicke lässt sich jeweils der Satz des Pythagoras anwenden:
gebildeten rechwinkligen Dreicke lässt sich jeweils der Satz des Pythagoras anwenden:
(2) ![]()
(3) ![]()
Auflösen der beiden Gleichungen nach ![]() und gleichsetzen, ergibt:
und gleichsetzen, ergibt:
(4) ![]()
Da ja ![]() ist, kann
ist, kann ![]() durch
durch ![]() ersetzt werden:
ersetzt werden:
(5) ![]()
Anwenden der binomischen Formel ergibt:
(6) ![]()
(7) ![]()
Addieren von ![]() auf beiden Seiten und ersetzen von
auf beiden Seiten und ersetzen von ![]() durch
durch ![]() , führt zu:
, führt zu:
(8) ![]()
Auflösen nach ![]() führt dann zu obigem Kosinussatz:
führt dann zu obigem Kosinussatz:
(9) ![]()