Trigonometrie: Sinus und Kosinus von 22,5 Grad

Es gelten bekanntlich folgende Zusammenhänge:

$\begin{equation*} \cos(\alpha + \beta)=\cos(\alpha)\cos(\beta) - \sin(\alpha)\sin(\beta) \end{equation*}$

$\begin{equation*} 1 = \cos^2(\alpha) + \sin^2(\alpha) \end{equation*}$

Damit ist auch:

$\begin{equation*} \cos(2\alpha)=\cos^2(\alpha) - \sin^2(\alpha) \end{equation*}$

$\begin{equation*} \sin^2(\alpha)= 1 - \cos^2(\alpha) \end{equation*}$

Ersetzen von $\sin^2(\alpha)$ in der vorletzten Gleichung, ergibt:

$\begin{equation*} \cos(2\alpha)=\cos^2(\alpha) - (1 - \cos^2(\alpha))=2\cos^2(\alpha) - 1 \end{equation*}$

Umstellen und auflösen nach $\cos(\alpha)$ :

$\begin{equation*} \cos^2(\alpha) = \frac{\cos(2\alpha)+1}{2} \end{equation*}$

$\begin{equation*} \cos(\alpha) =\sqrt{ \frac{\cos(2\alpha)+1}{2}} \end{equation*}$

Jetzt setzt man für $\alpha=\pi/8=22,5^\circ$ und kann den gesuchten Wert berechnen:

$\begin{equation*} \cos(\pi/8) =\sqrt{ \frac{\cos(\pi/4)+1}{2} }=\sqrt{ \frac{\frac{1}{\sqrt{2}}+1}{2} } \end{equation*}$

Dieser Ausdruck umgeformt:

$\begin{equation*} \sqrt{ \frac{\frac{1}{\sqrt{2}}+1}{2} } =\sqrt{ \frac{1 +\sqrt{2}}{\sqrt{2}} \cdot \frac{1}{2} }= \frac{ \sqrt{\sqrt{2}+2}}{2} \end{equation*}$

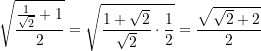
Der Sinus ergibt sich aus dem bekannten Additionstheorem:

$\begin{equation*} \sin(\alpha + \beta)=\sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta) \end{equation*}$

Einsetzen von $\alpha=\beta=22,5^\circ=\pi/8$ :

$\begin{equation*} \sin(45^\circ)=\sin(22,5^\circ)\frac{ \sqrt{\sqrt{2}+2}}{2} + \sin(22,5^\circ)\frac{ \sqrt{\sqrt{2}+2}}{2} \end{equation*}$

$\begin{equation*} \sin(45^\circ)=\sin(22,5^\circ) \sqrt{\sqrt{2}+2}} \end{equation*}$

Der Sinus von $45^\circ$ ist bekanntlich $1/\sqrt{2}$ . Damit erhält man:

$\begin{equation*} \frac{1}{\sqrt{2}}=\sin(22,5^\circ) \sqrt{\sqrt{2}+2}} \end{equation*}$

Der Sinus von $22,5^\circ$ ist damit:

$\begin{equation*} \sin(22,5^\circ) = \frac{1}{\sqrt{2} \cdot \sqrt{\sqrt{2}+2}}} = \frac{1}{\sqrt{2\sqrt{2}+4}}} \end{equation*}$